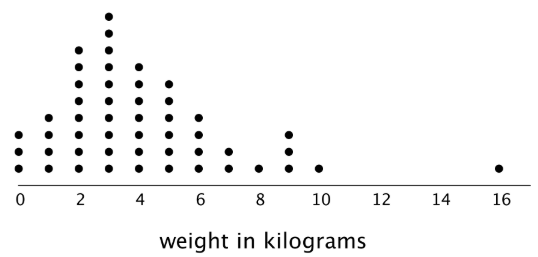

Let's use dot plots to describe distributions and answer questions. Exercise \(\PageIndex<1>\): Packs on Backs This dot plot shows the weights of backpacks, in kilograms, of 50 sixth-grade students at a school in New Zealand.
Do you agree with either of them? Explain your reasoning.
Exercise \(\PageIndex\): On the Phone
Twenty-five sixth-grade students were asked to estimate how many hours a week they spend talking on the phone. This dot plot represents their reported number of hours of phone usage per week.
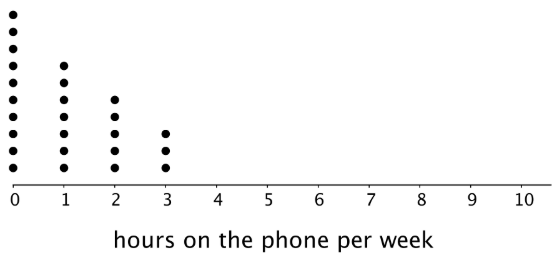
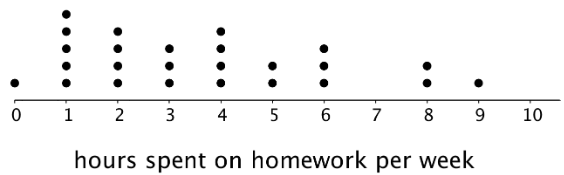
Overall, are these students more alike in the amount of time they spend talking on the phone or in the amount of time they spend on homework? Explain your reasoning.
Exercise \(\PageIndex\): Click-Clack

Based on the dot plots, do you agree with each of the following statements about this group of students? Be prepared to explain your reasoning.
Are you ready for more?
Use one of these suggestions (or make up your own). Research to create a dot plot with at least 10 values. Then, describe the center and spread of the distribution.
One way to describe what is typical or characteristic for a data set is by looking at the center and spread of its distribution.
Let’s compare the distribution of cat weights and dog weights shown on these dot plots.
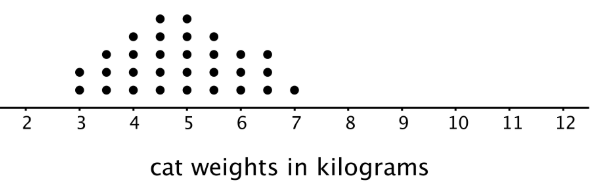
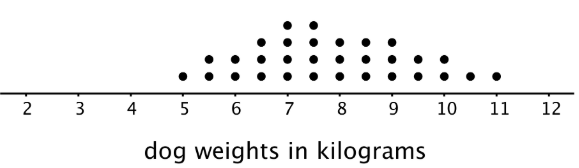
The collection of points for the cat data is further to the left on the number line than the dog data. Based on the dot plots, we may describe the center of the distribution for cat weights to be between 4 and 5 kilograms and the center for dog weights to be between 7 and 8 kilograms.
We often say that values at or near the center of a distribution are typical for that group. This means that a weight of 4–5 kilograms is typical for a cat in the data set, and weight of 7–8 kilograms is typical for a dog.
We also see that the dog weights are more spread out than the cat weights. The difference between the heaviest and lightest cats is only 4 kilograms, but the difference between the heaviest and lightest dogs is 6 kilograms.
A distribution with greater spread tells us that the data have greater variability. In this case, we could say that the cats are more similar in their weights than the dogs.
In future lessons, we will discuss how to measure the center and spread of a distribution.
The center of a set of numerical data is a value in the middle of the distribution. It represents a typical value for the data set.
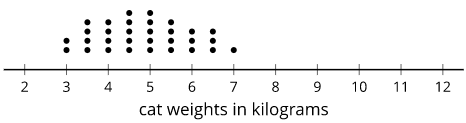
For example, the center of this distribution of cat weights is between 4.5 and 5 kilograms.
The distribution tells how many times each value occurs in a data set. For example, in the data set blue, blue, green, blue, orange, the distribution is 3 blues, 1 green, and 1 orange.
Here is a dot plot that shows the distribution for the data set 6, 10, 7, 35, 7, 36, 32, 10, 7, 35.
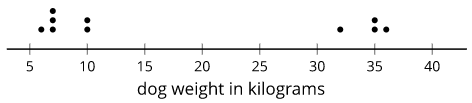
The frequency of a data value is how many times it occurs in the data set.
For example, there were 20 dogs in a park. The table shows the frequency of each color.
| color | frequency |
|---|---|
| white | \(4\) |
| brown | \(7\) |
| black | \(3\) |
| multi-color | \(6\) |
The spread of a set of numerical data tells how far apart the values are.
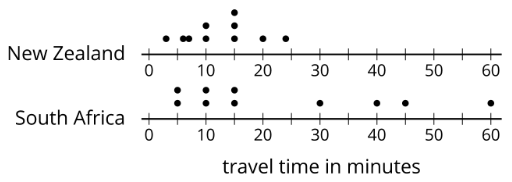
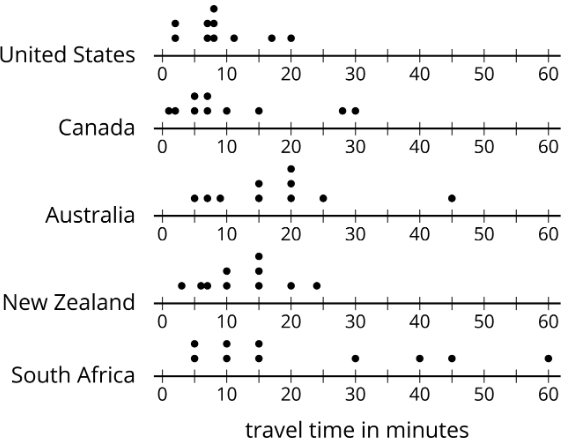
For example, the dot plots show that the travel times for students in South Africa are more spread out than for New Zealand.
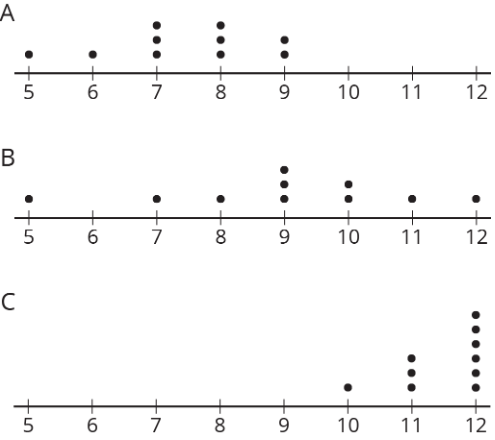
Three sets of data about ten sixth-grade students were used to make three dot plots. The person who made these dot plots forgot to label them. Match each dot plot with the appropriate label.
The dot plots show the time it takes to get to school for ten sixth-grade students from the United States, Canada, Australia, New Zealand, and South Africa.
Twenty-five students were asked to rate—on a scale of 0 to 10—how important it is to reduce pollution. A rating of 0 means “not at all important” and a rating of 10 means “very important.” Here is a dot plot of their responses.
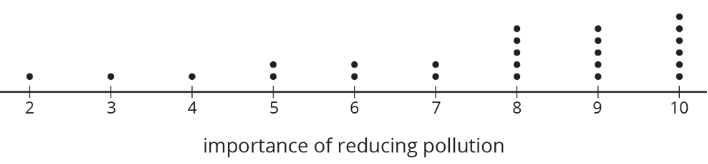
Explain why a rating of 6 is not a good description of the center of this data set.
Tyler wants to buy some cherries at the farmer’s market. He has $10 and cherries cost $4 per pound.
42.3: Using Dot Plots to Answer Statistical Questions is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by LibreTexts.